機械設計者として就職したのはいいけど、いきなり材料の強度計算を求められてびっくりしている初心者技術者の方！そんなあなたに向けて、材料力学の基礎をわかりやすく解説します。もちろん、ベテラン技術者の方も復習がてら参考にしてくださいね。この記事を読めば、材料力学の超基礎である「4つの応力」や「断面二次モーメント」「断面二次極モーメント」の成り立ちがスッキリ理解できるようになりますよ！
『人生をゆるく 楽しく ダンディに ストレスなく生きる』方法を発信します！
今回はは4つの応力を復習します！いきなりまとめです！
材料力学では「4つの応力」を押さえるのが基本中の基本です。これから説明する式も載せますね。
- 引張応力
- 圧縮応力
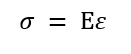
- せん断応力
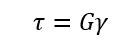
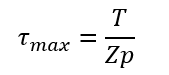
- 曲げ応力
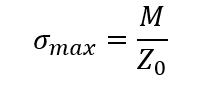
これらを覚える順番としては、まず「引張」と「圧縮」が簡単。次に「せん断」、最後に「曲げ」と考えましょう。それでは、簡単なものから順番に詳細を説明していきます。
応力とひずみの基本は、引張応力と圧縮応力
4つの応力を説明する前にまずは応力とひずみの基本について復習しましょう。
材料に力を加えると伸び(記号δ(デルタ):単位mm)が起こります。この伸びを元の長さ(記号l:単位mm)で割ったものが ひずみ(記号ε(イプシロン):単位 無次元量) です。なぜひずみで表すかというと材料の伸びがどこでも同じ割合で伸びていると考えるからです。
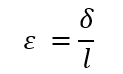
次に重要になってい来るのは応力(記号σ(シグマ):単位 Pa)です。材料に加わる力(記号P:単位 N)を断面積(記号A:単位 mm2)で割った値になります。単位面積分の力の量を示しているんですね。
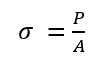
そして、棒を引張試験または圧縮試験を行って応力とひずみの関係をグラフにすると下の図のようになります。
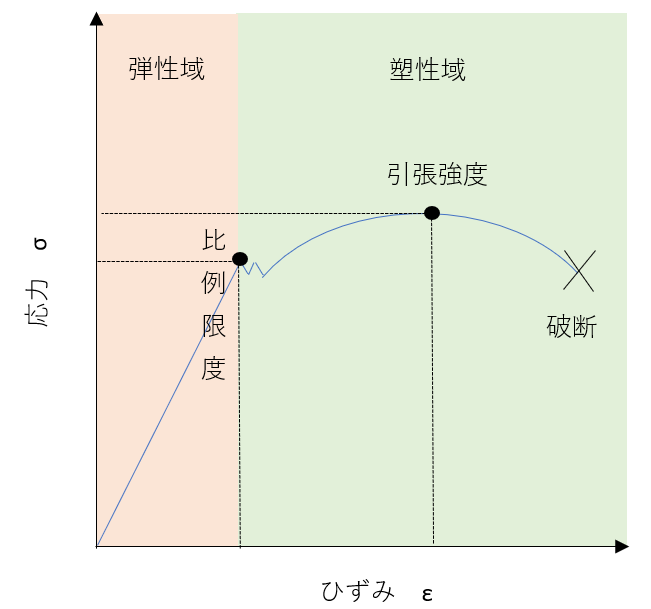
で、機械設計で使う応力はほとんどの場合 弾性域を使います。弾性域は線形なので解析でいう線形解析というのはここの範囲の解析のことです。
弾性域上では、材料力学で超重要な フックの法則 が成り立ちます。弾性域の傾きをヤング率(記号E:単位 Pa)といいます。つまり応力は下のようにも表せます。
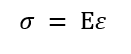
この関係が成り立つのは材料が「弾性変形」している範囲内だけですが、ほとんどの設計計算ではこれを使います。この応力でひずみが正 つまり伸びているときは引張応力、ひずみが負 つまり縮んでいるときは圧縮応力といいます！
フックの法則の考え方が本当に材料力学の基礎だと思っています。
せん断応力もフックの法則！
次にせん断応力(記号 τ(タウ):単位 Pa)です。そもそもせん断応力というのは例えるなら、大根を包丁で切ったときの包丁の力を大根の断面積で割った値と考えてください。(大根でなくてもいいけど笑)
しかも、せん断応力もひずみと関係し、以下のフックの法則が成り立つんです！しかしひずみはδではなくɤ(ガンマ)で表し、係数もEではなくて横弾性係数(記号 G:単位 Pa)になります。式で表すと以下になります。
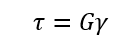
せん断応力もフックの法則なので単純に掛け算なんですよー！
せん断応力の応用編 丸棒とねじり
ここからせん断応力をもう少し掘り下げて、便利にしていきます。先に結論から言うとGがわからなくても丸棒の部品であればトルクを使ってせん断応力が求まっちゃうんです！これには断面二次極モーメントを用います！楽しくなってきましたね。でもここがつまずくポイントなんですよ。頑張りましょう。
丸棒にねじりを加えた場合、ねじれた角度をΘとすると、ひずみはrΘと表せます。すると上の式は下のようにもなりますね。
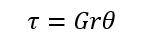
ココからもっとポイントです！ねじれた丸棒の断面を見てみると外側ほどねじれが大きく中心は全くねじれていません。ねじれているということはトルクが発生していますが、このトルクは微小のトルクの足し算、、、つまり積分した値になります！ではまず、微小のトルクを求めましょう。
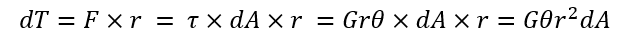
積分すると
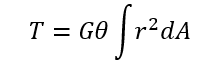
ここで
を活用します。これが断面二次極モーメントです！さらにτ = GrΘからGΘ = τ/r を活用すると
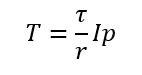
素晴らしい！Gが消えました！さらにこれを応力に変換していくと
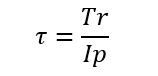
超最高！せん断応力がトルクと半径と断面二次極モーメントで表せましたね！そしてもっともっとせん断応力を簡単に表していきますよ。Ip/r = Zp 極断面係数 (※このときのrは丸棒の外形とします)とおきます。すると最大せん断応力は下のようになります。
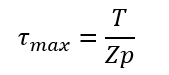
せん断応力がトルクを極断面係数で割った値になりました。ただの割り算になってしまうんですね。すごく便利！そして簡単ですよね！
曲げ応力と断面二次モーメント
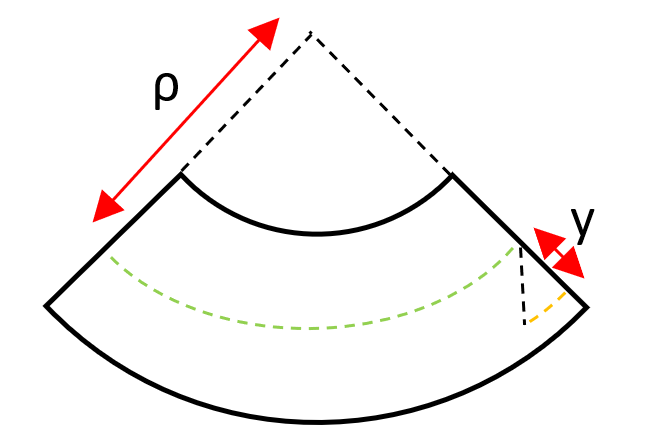
最後に「曲げ応力」です。これは梁（はり）にかかる曲げモーメント M を使って計算されます。曲げモーメントというのは、そんなに難しく考えなくてよくてただのモーメントと考えておっけいです。力×距離ですね。下の超基礎の固定端の片持ち梁では、最大の曲げモーメントは根元の箇所で値はM=WLです！
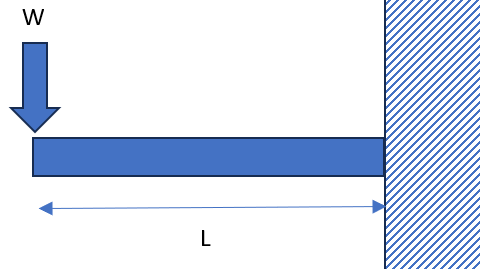
梁の曲がった部分に着目して、曲げによって生じたひずみをy/ρとしててみます。どういうことかというと下の図を見てください。曲げた梁を表しています。緑の点線は曲げの中立面つまり、圧縮も引張もかからないところです。中立面より下は引張の力が加わり、中立面より上は圧縮が加わっています。この関係から緑の点線の長さが元の長さでオレンジの点線の長さが伸びになります。(あんまり深く考えなくていいですよ。)
この関係からフックの法則を変換します。
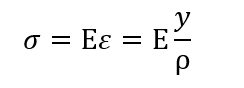
それではここで微小の曲げモーメントを考えます。
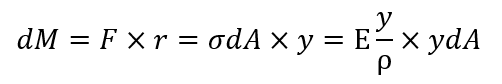
積分していきます。
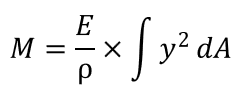
ココでやっと出てきました
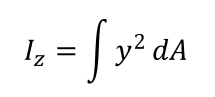
とおきます。これが断面二次モーメントになります！これを使うと
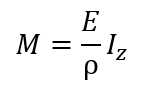
これをE/ρ = M/Izと変換して応力に代入すると
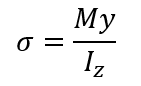
さらにも最大曲げ応力を簡単な式にしていきますよ。たいていの断面の形状は中立面を境に対象であることがほとんどです。そのためyは大体決まってきます。そこで、Iz/y = Z0 断面係数(※ここでyはy軸の最大の距離)と置くと
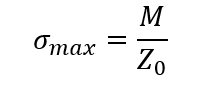
はい。超最高！またまた最大曲げモーメントを断面係数で割るという簡単な式で最大の曲げ応力を求めることができました。Eも入っていません！これで計算がグッと楽になります！
まとめ
この記事では、材料力学の基礎である「4つの応力」の考え方と成り立ちを説明しました。以下が今回のポイントです：
- 応力とひずみの関係はフックの法則が基本！これで基本的な応力が求まる！
- 丸棒においては極断面係数を用いることで簡単に最大せん断応力を求められる！
- 断面係数を用いることで簡単に最大曲げ応力が求められる！
これをしっかり理解すれば、材料力学の基礎計算はもう怖くありません！ともに設計業務を頑張っていきましょう！！
大学で習った知識をこちらの記事で復習できたのではないでしょうか！成り立ちがわかるとちょっと賢くなった気分になりますよね♪
